One way to speed up your code is to remove any unnecessary work. This may sound so obvious but in reality it is quite difficult to spot it and remove it.
Consider the following code snippet. Do you see any unnecessary work we are doing?
#include <vector>
#include <cassert>
template<typename T>
auto operator+(std::vector<T> const& xs, std::vector<T> const& ys) {
assert(xs.size() == ys.size());
std::vector<T> result;
result.reserve(xs.size());
for (std::size_t idx = 0; idx < xs.size(); ++idx)
result.push_back(xs[idx] + ys[idx]);
return result;
}
int main() {
std::vector<int>xs{1,2,3};
std::vector<int>ys{10,20,30};
auto sum = xs + ys;
}
Well, it is not so obvious, is it? The potential problem of the code isn’t going to be easy to spot. In fact, the code above itself is probably OK, but it poses a serious inefficiency as soon as we do things like
auto sum = xs + ys + zs;
That is when we use operator+() multiple times in a single expression. What is the problem? The operator+() function instantiates a new vector, which is expensive as it requires dynamic allocation. The expression xs + ys + zs therefore instantiates the vector two times, one for each operation, roughly equivalent to below:
// temp = xs + ys
std::vector<int> temp;
temp.reserve(xs.size());
for (auto i = 0; i < xs.size(); ++i) temp.push_back(xs[i] + ys[i]);
// result = temp + zs
std::vector<int> result;
result.reserve(result.size());
for (auto i = 0; i < result.size(); ++i) result.push_back(temp[i] + zs[i]);
You can easily imagine that in a complex mathematical expression that involves a bunch of these inefficient operation can easily cost you a lot, because ideally you want to instantiate the result vector only once.
The problem is that we are too eager to calculate the addition as soon as we see the operator+() method. Once we calculate it, we have to store it, so that is why we instantiate vector to store the result.
It is time to be a bit lazy. Let’s not carry out the operation until we are forced to do so. Rather than storing the actual sum, we can create a temporary object, which delays its work until the last minute when the result is explicitly required when someone calls its operator[]() method. The desired end result should be roughly equivalent to:
// result = xs + ys + zs
std::vector<int> result;
result.reserve(xs.size());
for (auto i = 0; i < xs.size(); ++i)
result.push_back(xs[i] + ys[i] + zs[i]);
Internally, we save references to its operands so that we can do the work later. Let’s call this class VectorSum. Note that we need to support nested call of operator+() on VectorSum object itself. For that, we need to create a simple vector-like-interface which must be satisfied by a normal vector class as well as VectorSum class. Let’s write in code.
template <typename T> struct VectorInterface {
virtual std::size_t size() const = 0;
virtual T operator[](std::size_t idx) const = 0;
};
template <typename T> struct VectorSum : VectorInterface<T> {
VectorInterface<T> const &x;
VectorInterface<T> const &y;
VectorSum(VectorInterface<T> const &x, VectorInterface<T> const &y)
: x{x}, y{y} {
assert(x.size() == y.size());
}
virtual std::size_t size() const { return x.size(); }
virtual T operator[](std::size_t idx) const { return x[idx] + y[idx]; }
};
template <typename T> struct Vector : VectorInterface<T> {
std::vector<T> data;
Vector() = default;
Vector(VectorInterface<T> const &v) {
data.reserve(v.size());
for (std::size_t idx = 0; idx < v.size(); ++idx)
data.push_back(std::move(v[idx]));
}
virtual std::size_t size() const { return data.size(); }
virtual T operator[](std::size_t idx) const { return data[idx]; }
};
template <typename T>
auto operator+(VectorInterface<T> const &x, VectorInterface<T> const &y) {
assert(x.size() == y.size());
return VectorSum<T>{x, y};
}
int main() {
Vector<int> xs; xs.data = {1,2,3};
Vector<int> ys; ys.data = {10,20,30};
Vector<int> sum = xs + ys;
}
Note that we also created a simple wrapper Vector class that is a subclass of VectorInterface. Now, let’s measure its runtime and see how much faster it can run. Below chart shows runtime for adding 10 vectors of type double of various sizes
std::vector<int> result = x1 + x2 + x3 + ... + x10;
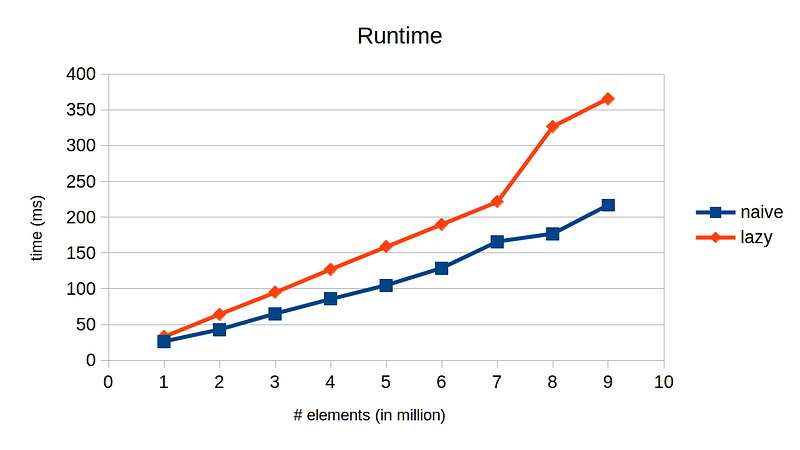
What just happened? The lazy evaluation technique is even slower! Why is this? With our implementation, the main bottleneck is that we need to call virtual function operator[]() millions of times. We know that virtual calls require dynamic dispatch, which adds slight inefficiency. More importantly, this prevents the compiler from optimizing the code because inline is no longer possible.
How can we solve this? The answer is static dispatch through templates. Rather than using class inheritance as an explicit interface, we can use templates for implicit interface. That is, we know what the interface is and create classes that satisfy the interface, but we never explicitly inherit the interface. Let’s write in code.
template <typename E1, typename E2> struct VectorSum {
E1 const &x;
E2 const &y;
VectorSum(E1 const &x, E2 const &y) : x(x), y(y) {}
auto size() const { return x.size(); }
auto operator[](std::size_t idx) const { return x[idx] + y[idx]; }
};
template <typename T> struct Vector {
std::vector<T> data;
Vector() = default;
template <typename E> Vector(E &&expr) {
data.reserve(expr.size());
for (std::size_t idx = 0; idx < expr.size(); ++idx) {
data.push_back(std::move(expr[idx]));
}
}
auto operator[](std::size_t idx) const { return data[idx]; }
auto size() const { return data.size(); }
};
template <typename E1, typename E2> auto operator+(E1 const &xs, E2 const &ys) {
return VectorSum<E1, E2>(xs, ys);
}
int main() {
Vector<int> xs; xs.data = {1,2,3};
Vector<int> ys; ys.data = {10,20,30};
Vector<int> sum = xs + ys;
}
We replace VectorInterface with template E where E satisfies the interface implicitly, i.e., has methods size() and operator[](). This technique is called expression templates. Oh by the way, this technique is widely popular in linear algebra libraries, such as Eigen and Boost uBLAS, where high performance is a must.
If you want to make it more explicit, you can use curiously recurring template pattern (CRPT) as shown here, but personally I think it makes code way too complicated and is an overkill for our simple scenario. Let’s benchmark our shiny new solution.
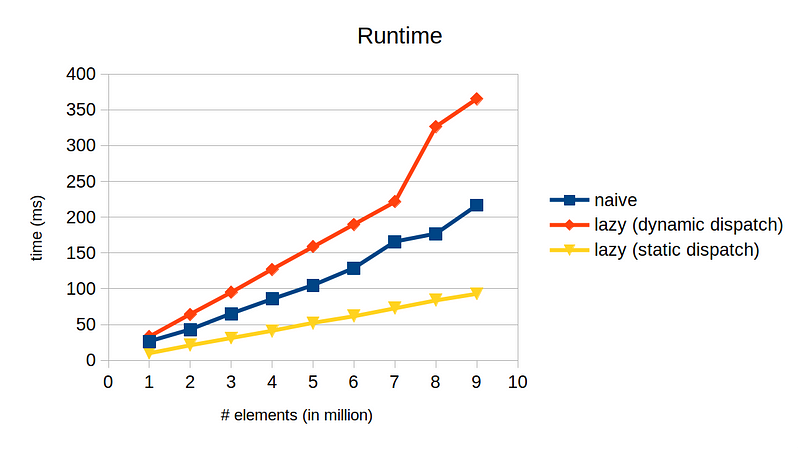
OK, now this looks promising. We are seeing 2x speed up! Now we know, the lazier the faster. The source code is available here.